As a global leader in superconducting quantum computing, we are on the path to developing industrial-relevant quantum computers within the next decade, as outlined in our development roadmap.
Our hardware focus is on superconducting quantum circuits (SQC) because they offer design flexibility which allows tailoring the quantum processing unit (QPU) connectivity to fault tolerance (FT) while providing state-of-the-art performance and scalable fabrication methods.
The field of SQC is already strong and well developed from proof-of-concept demonstrations to large-scale engineering projects. With these strengths, we are designing innovative superconducting QPUs based on the best quantum error-correcting codes known today, whilst actively looking for even more efficient alternatives.
Currently, the most investigated code for SQC is the surface code [1], which suffers from a low encoding rate and, hence, a physical-to-logical qubit ratio on the order of 1000 or worse. To overcome this limitation, we have identified a family of QEC codes that outperforms the surface code, namely quantum Low-Density Parity-Check (qLDPC) codes with high local or near-local connectivity, i.e., weight-6 stabilizers, or higher, without the need of periodic boundary conditions. Comparing qLDPC codes against the surface code shows potential savings of a factor of 10 in the number of physical qubits, as well as additional advantages due to more resource-efficient fault-tolerant operations.
In this way, the resource requirements of industrial-relevant quantum computers can be sufficiently lowered to enable an implementation by the end of the decade. Such QEC codes require, amongst other enabling technologies, QPUs with novel inter-qubit connectivity.
Surface codes provide a clear and straight forward path to fault-tolerant quantum computing under the price of a prohibitive qubit overhead. Compared to the surface code, so-called quantum Low-Density Parity-Check (qLDPC) codes may provide an alternative route circumventing the qubit overhead issue and better protection of encoded qubits. However, realizing the promises of qLDPC codes is far from trivial since qLDPC codes with the best theoretical performance are inherently non-2D.
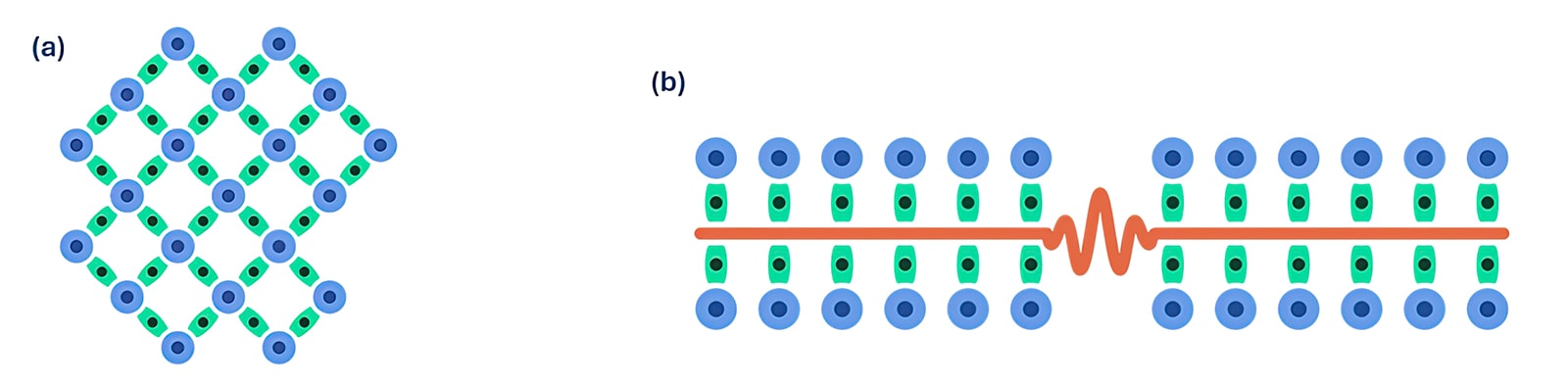
Figure 1 – IQM’s QPU topologies. Basic building blocks are flux-tunable superconducting transmon qubits (blue dots), flux-tunable couplers (green rectangles) and computational resonators (red line). (a) IQM Crystal-20 QPU with nearest neighbor coupling. (b) IQM Star-24 QPU, where all qubits are coupled to a central resonator.
By cleverly designing quantum codes with a modest increase in non-locality compared to the surface code, we can achieve substantial performance gains. However, a key challenge remains: developing hardware that can efficiently implement these codes with reduced connectivity complexity. To address this, we implement a suitable combination of IQM’s Crystal and Star topologies, which balance high parallelism and connectivity, enabling the scalable implementation of qLDPC codes.
The key to building industrial-relevant quantum computers is a continuous effort to reduce the required number of physical qubits for a given performance level. Beyond the above-mentioned surface codes, we plan to unlock higher encoding rates by exploring and implementing more resource-efficient variants of the large qLDPC code family.
To this end, we created a new family of qLDPC codes called Tile Codes [2]. These codes aim to bridge the gap between the low-overhead qLDPC codes and the high degree of physical locality inherent in the surface code. The primary contribution is a systematic and scalable method for constructing planar stabilizer codes with open boundaries and constant-weight local checks, while encoding significantly more logical qubits than conventional surface codes of comparable size.
In particular, our findings suggest that a significant reduction (>10x) in the number of physical qubits can be achieved by allowing for near-local connectivity beyond nearest neighbors. Such “near-local connections” (NLC) typically extend over a few lattice sites and must be implemented in a translationally invariant manner across the bulk of the QPU.
NLCs will likely require additional high-quality surfaces in the QPU stack and high-quality connection elements between these surfaces. Fundamentally, the fabrication of NLCs is conceivable in the next decade, to keep the fabrication complexity of an industrial-relevant quantum computer as low as possible, it is thus desirable to reduce length and the number of NLCs as much as possible. The combined crystal-star topology provides a clear path for reducing the requirement on NLC.
Focusing on reducing the complexity of qLDPC codes, IQMs approach of designing tile codes shows a methodology that is modular, transparent, and readily extensible. It supports flexible choices of tile size, stabilizer weight, and lattice geometry—including the incorporation of holes or rotated patches—without compromising physical locality. Most importantly, its systematic tiling and boundary pruning procedures yield codes with open boundaries, overcoming the architectural complexity often associated with qLDPC code constructions.
IQM’s approach to error correction preserves approximate physical locality by confining every stabilizer measurement to bounded, constant-size tiles, mirroring the key locality structure of the patch-based surface code. Therefore, we have a tile-like assembly and support straightforwardly, purely local (physical and logical) operations such as lattice-surgery techniques [3,4]. Their localized stabilizer interactions and planar boundary conditions mean that they can be deployed interchangeably with traditional patches: they support equivalent syndrome extraction circuits, merge/split operations for lattice surgery, and modular block configurations—while delivering a significantly higher logical-qubit density and maintaining compatibility with existing surface-code tooling and methodology.
Our framework delivers a compelling compromise between the high density of qLDPC codes and the stringent locality of surface codes. For quantum error correction initiatives focused on near‑term demonstrations, our approach offers a structured, hardware‑friendly path to high‑efficiency and feasable fault‑tolerance quantum computing on SQC.
As researchers and engineers continue advancing the frontier of fault-tolerant quantum computing, a central challenge remains: the development of efficient architectures and protocols that operate within locality and complexity constraints. While complexity constraints are universal—every problem admits both optimal and suboptimal solutions—locality constraints arise predominantly from limitations of hardware platforms. In particular, superconducting quantum circuits, despite being significantly faster than alternative quantum platforms, impose strict locality limitations due to fabrication constraints.
At IQM, we embrace these challenges as an opportunity for innovation. By leveraging our full-stack approach to quantum computing, we are uniquely positioned to optimize every layer of the quantum computing stack—from theoretical protocols to hardware implementation—delivering integrated and efficient solutions to some of the most complex challenges in the field.
A prime example is our development of fault-tolerant architectures based on quantum low-density parity-check (qLDPC) codes. Starting from a theoretical foundation, our team has significantly reduced the implementation complexity of qLDPC codes through the introduction of tile codes. These modular, hardware-aware constructions serve as a bridge between theory and practice, allowing us to fine-tune fabrication parameters and develop customized control technologies, ultimately maximizing performance on our superconducting QPUs.
This integrated approach also extends to fault-tolerant protocols with reduced space-time complexity. A critical step toward scalable quantum computation is the design of protocols implementing a universal gate set. Unlike other qLDPC constructions, Tile codes are naturally suited to support lattice surgery in a surface-code-like framework. This compatibility enables us to implement intuitive, dynamic, and highly efficient protocols for logical operations.
One of the central challenges in realizing universal fault-tolerant quantum computation with qLDPC codes lies in the implementation of non-Clifford gates, such as the T gate. While Clifford gates can often be implemented transversally or via low-overhead lattice surgery, non-Clifford gates typically require resource-intensive procedures like magic state distillation, which introduce significant space-time overhead.
To solve this problem, new strategies are being explored, including gauge fixing [5] and specialized magic state protocols on other types of codes [6-8]. Solving the non-Clifford gate problem is an essential and well-known problem for unlocking the full potential of qLDPC codes in universal fault-tolerant quantum computing where the whole community is working together.
By combining the spatial efficiency of tile codes with the temporal advantages of direct lattice surgery, IQM achieves an exceptionally low space-time overhead—placing us at the forefront of practical, scalable, fault-tolerant quantum computing. One key challenge remains: decoding.
As we move forward with quantum LDPC (qLDPC) codes, we also take on the open problems they bring. Until recently, it was widely believed that the decoding complexity inherent to qLDPC codes would pose a fundamental obstacle to universal fault-tolerant quantum computation. This challenge stems from the degeneracy of qLDPC codes, which causes standard belief propagation (BP) decoding to perform sub-optimally.
Although several enhanced decoding schemes have been proposed—such as BP-OSD, which uses Ordered Statistics Decoding as a post-processing step—these often come with steep computational costs [9,10]. In particular, OSD involves inverting a full-rank submatrix of the parity-check matrix, resulting in a decoding complexity of 𝑂(𝑚3), where 𝑚 is the number of faulty locations on a QEC cycle—a number that can far exceed the number of physical qubits.
To address this, researchers have proposed a number of variations and enhancements to the BP algorithm. Some of these sacrifice performance to gain speed; others achieve both efficiency and accuracy [11,12]. Recent breakthroughs have demonstrated that decoding qLDPC codes can indeed be performed in polynomial time without sacrificing reliability—dismantling a long-standing barrier to practical implementations.
At IQM, we build on this progress by collaborating with leading experts and companies who bring decades of experience in decoding algorithms [13]. Together, we are developing a highly integrated, accurate and fast decoding solution. This marks a pivotal step toward full-stack, fault-tolerant quantum systems that are truly deployable.
Ultimately, the development of a fault-tolerant architecture under locality and complexity constraints will require a multidisciplinary approach that brings together expertise from a range of fields, including quantum error-correction, chip-design, and fabrication.
By working together in an open and collaborative environment, IQM is developing innovative solutions to these challenges, creating fault-tolerant quantum computers that are fast, resilient, robust, and capable of solving industrial-scale problems. This unique approach has the potential to revolutionize fault-tolerant quantum computing and could have a significant impact on our daily lives and the world around us.
In a highly dynamic field such as quantum computing, plausible plans made today will need to be constantly adjusted to future novel and disruptive findings. Our roadmap provides the flexibility to ensure the best possible synergy between progress in hardware scaling and QEC code engineering. In this way, we mitigate the risk that a competitive approach achieves a massive breakthrough to which it would take us a long time to react.
[1] A. Fowler, et al., “Surface codes: Towards practical large-scale quantum computation,” Physical Review A 86, 032324 (2012). DOI: https://journals.aps.org/pra/abstract/10.1103/PhysRevA.86.032324
[2] V. Steffan, et al., “Tile Codes: High-Efficiency Quantum Codes on a Lattice with Boundary,” https://arxiv.org/html/2504.09171v1, 2025.
[3] D. Litinski, “A Game of Surface Codes: Large-Scale Quantum Computing with Lattice Surgery,” Quantum, vol. 3, p. 128, 2019.: https://quantum-journal.org/papers/q-2019-03-05-128/
[4] Yingli Yang, Guo Zhang, and Ying Li, “Planar Fault-Tolerant Quantum Computation with Low Overhead”, https://arxiv.org/abs/2506.18061, 2025.
[5] H. Bombín, Gauge color codes: optimal transversal gates and gauge fixing in topological stabilizer codes, New Journal of Physics 17 083002 (2015). DOI: https://www.researchgate.net/publication/280970985_Gauge_color_codes_Optimal_transversal_gates_and_gauge_fixing_in_topological_stabilizer_codes
[6] S.-H. Lee, “Low-overhead magic state distillation with color codes,” https://arxiv.org/abs/2409.07707, 2024.
[7] Z. Chen, et al., “Efficient Magic State Cultivation on RP²”, https://arxiv.org/abs/2503.18657, 2025.
[8] C. Gidney, et al., “Magic state cultivation: growing T states as cheap as CNOT gates”, https://arxiv.org/abs/2409.17595, 2024.
[9] P. Panteleev and G. Kalachev, “Degenerate Quantum LDPC Codes with Good Finite‑Length Performance”, Quantum 5, 585 (2021). DOI: https://arxiv.org/abs/1904.02703
[10] J. Roffe, et al., “Decoding across the quantum low-density parity-check code landscape”, Physical Review Research, 2, 043423 (2020). DOI: https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.043423
[11] A. iOlius, et al., “An almost-linear time decoding algorithm for quantum LDPC codes under circuit-level noise”, https://arxiv.org/pdf/2409.01440, 2024.
[12] T. Müller, et al., “Improved belief propagation is sufficient for real-time decoding of quantum memory”, https://arxiv.org/pdf/2506.01779, 2025.
[13] F. Martínez‑García, at al., “Near‑optimal decoding algorithm for color codes using Population Annealing”, https://arxiv.org/abs/2405.03776, 2024

Dr. Francisco Revson Fernandes Pereira is the Team Leader for Quantum Error Correction Theory at IQM Quantum Computers, focusing on practical fault tolerance for superconducting processors. His work spans the design and analysis of error-correcting codes, scalable decoding algorithms for large code blocks, and fault-tolerant algorithms. He completed his PhD in Brazil, where he focused on AG constructions for quantum and entanglement-assisted codes; during his PhD he was a visiting researcher at Eindhoven University of Technology under Ruud Pellikaan. Before joining IQM, he was a postdoctoral fellow in Stefano Mancini’s group at the University of Camerino. Since 2022, he has been at IQM assisting the development of QEC research from theory to experiments. Outside of research, he enjoys hiking, cycling, and playing the trumpet.
Search faster—hit Enter instead of clicking.