
Current superconducting quantum processors are mostly built using a square lattice topology, where each qubit connects to four nearest neighbors. This architecture is a natural fit for surface code quantum error correction (QEC). While powerful, surface code demands a vast number of physical qubits to protect even a small number of logical qubits.

Fig 1: IQM Crystal, a square lattice topology
Alternative codes, such as color codes and quantum low-density parity check (qLDPC) codes, promise to encode more logical qubits with fewer physical qubits. However, these codes are not well-suited to the native connectivity of square lattice architectures. This gap motivated the development of a new processor design, known as IQM Constellation.
Every quantum gate operation performed today has an error probability around 10⁻³. Large-scale quantum algorithms require error probabilities below 10⁻¹⁰. Reducing this gap demands quantum error correction.
QEC efficiency depends strongly on the native qubit connectivity. Superconducting qubits can only perform gate operations with qubits they are physically connected to. The architecture of those connections directly shapes what codes and operations can run efficiently.
IQM previously developed IQM Star, a processor where qubits are connected to a central resonator. This star topology creates effective all-to-all connectivity within a star. While it offers flexibility for two-qubit gates between distant qubits, it has limited parallelism.

Fig 2: IQM Star
Because all multi-qubit operations pass through the central resonator, only one operation can run at a time in the IQM Star. This bottleneck slows down QEC cycles, especially as the number of qubits grows. The challenge was to keep the connectivity advantages of a star topology but allow scalable parallel operations.
IQM Constellation utilizes a star lattice architecture, built from cells with star connectivity. This design lets the degree of parallelism and local connectivity be tuned by changing how many qubits are in each star. A key example is the six-qubit star lattice, which consists of hexagonal cells of six qubits connected to a central resonator.
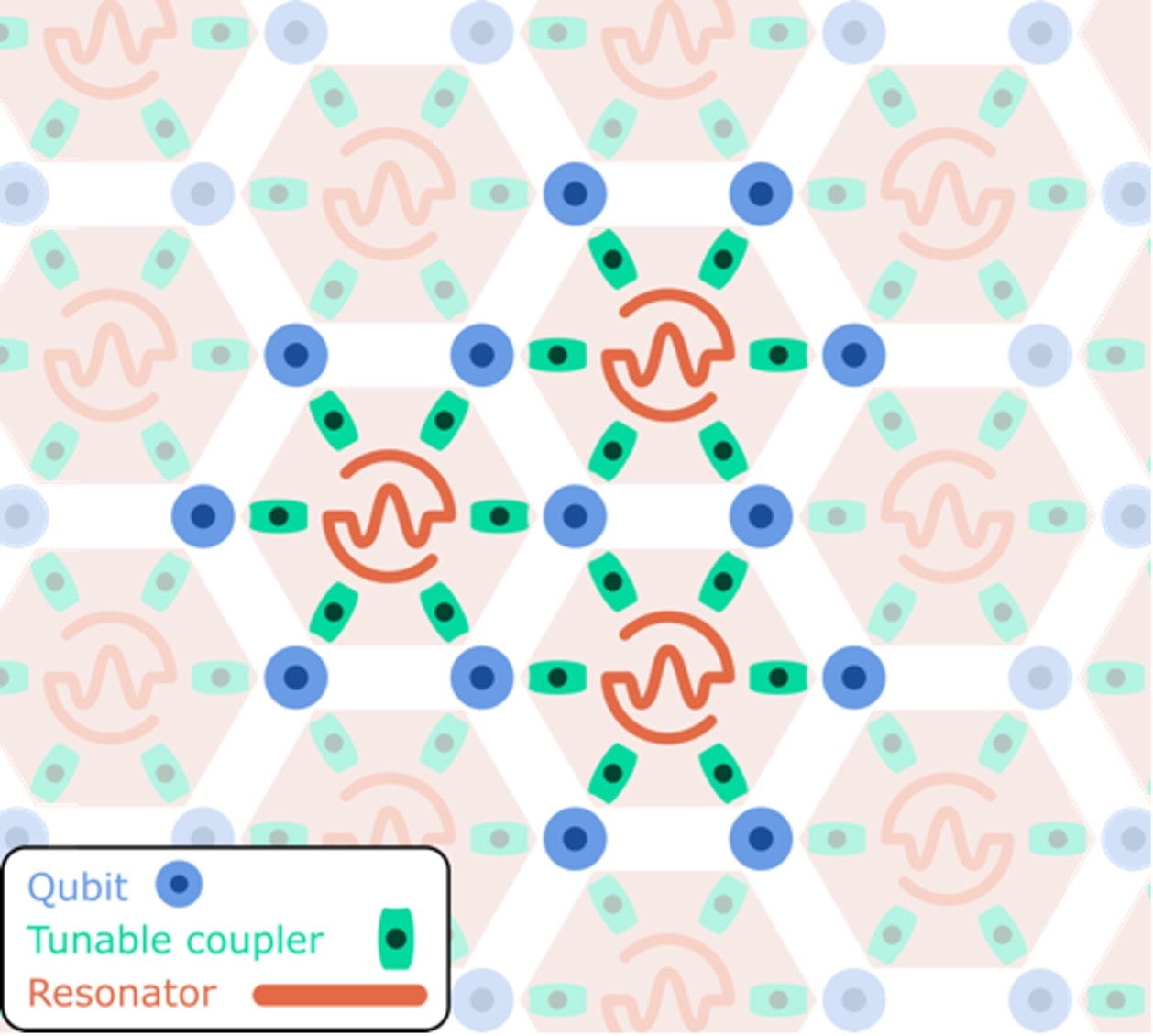
Fig 3: IQM Constellation
Regarding connectivity and parallelism, it provides an optimal trade-off because each unit cell associates two qubits to one coupling resonator. In this way, one achieves strong local connectivity while allowing all qubits to be engaged in parallel operations.
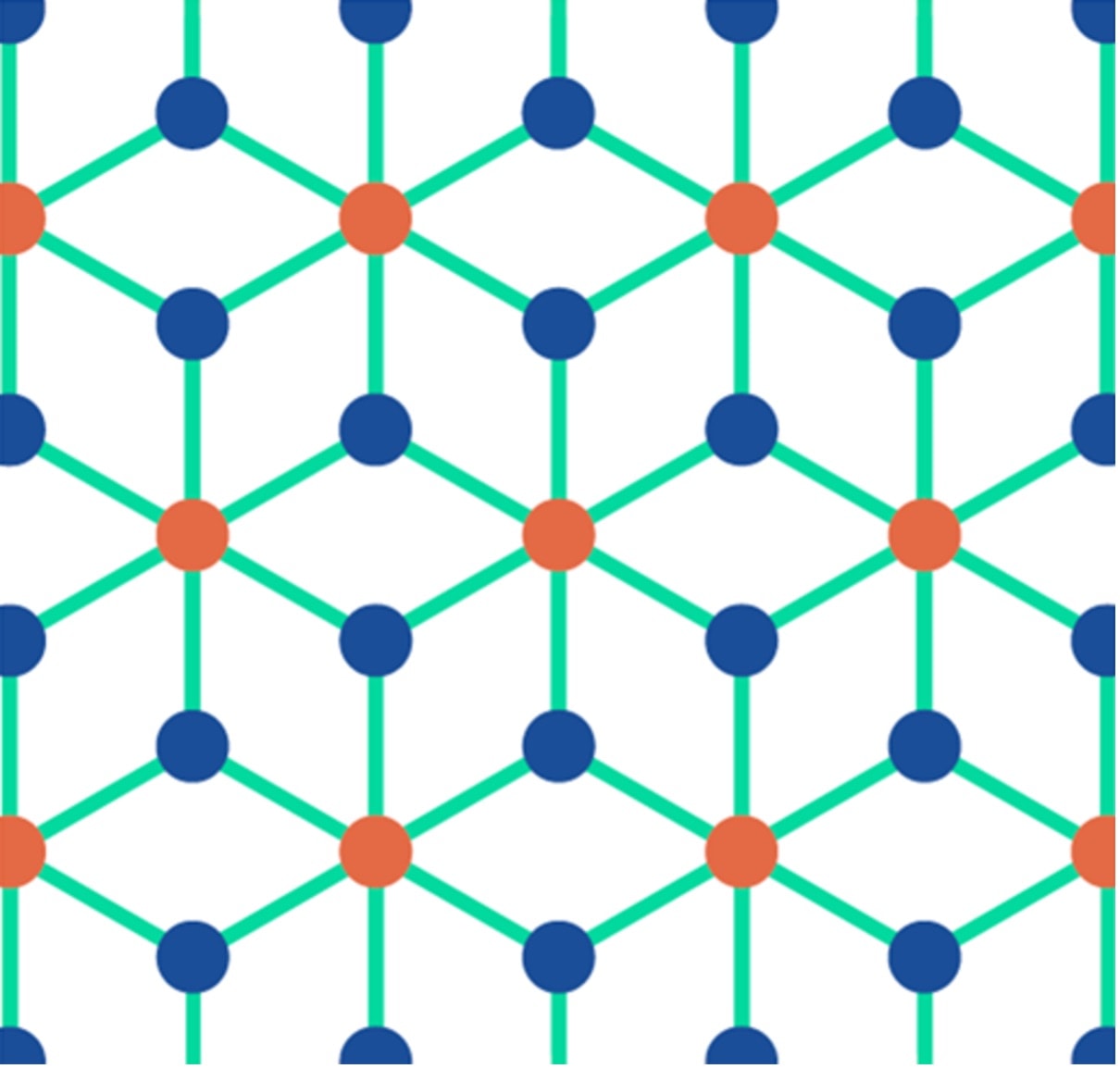
Fig 4: Bipartite rhombille graph
IQM Constellation inherits and extends gate protocols optimized for IQM Star. Two key operations:
A sequence of MOVE–CZ–MOVE produces a high-fidelity CZ gate between any two qubits inside a star. Fidelities above 99.3% have been achieved using this protocol.
In the six-qubit star lattice, every qubit connects to all other qubits in its star, forming a dense hexagonal graph. At a given time, only one two-qubit gate can run per star, but with one star for every two qubits, parallelism remains high across the processor.
Quantum architectures must trade off connectivity with parallelism. Few stars with many qubits maximize connectivity but restrict simultaneous operations. Many stars with few qubits maximize parallelism but limit connectivity.

Fig 5: Connection graph
The six-qubit star lattice strikes a strong balance:
IQM is constantly working on improving the performance of its quantum processors. Work is also underway to test quantum error correction codes that fully exploit the architecture’s connectivity advantages.
Surface code on square grids has been investigated and refined for over a decade. High-connectivity QEC codes optimized for star lattices remain an exciting open field for research and development. IQM invites the research community to explore this new design space and follow upcoming results and publications.
Reference: Quantum error detection in qubit-resonator star architecture. arXiv:2503.12869

Florian Vigneau is a quantum engineer with a background in quantum devices and experimental physics. In the quantum error correction integration team at IQM, he works hand-in-hand with theoreticians and engineers from the all-quantum computing stack to make fault-tolerant quantum computers a reality.
Search faster—hit Enter instead of clicking.