QEC will be the key to making quantum computers reliable enough for practical applications. Because qubits are highly sensitive to noise, a QEC code protects quantum information by encoding a logical qubit into several physical qubits. This redundancy enables error detection and correction without disturbing the computation. Finding codes that offer strong protection while keeping hardware demands low is one of the key challenges in realizing large-scale quantum computing.

A QEC code can be characterized by its three code parameters: [[𝑛, 𝑘, 𝑑]]. Here, 𝑛 is the number of physical qubits used, 𝑘 is the number of logical qubits encoded, and 𝑑 is the code distance—a measure of how many errors the code can detect and correct: A larger distance 𝑑 means stronger error correction capabilities. The goal is to maximize both 𝑘 and 𝑑 while minimizing 𝑛, achieving efficient encoding with strong error correction capabilities and low qubit overhead. One challenging constraint is that the connectivity required by the QEC code must match the one of the chip one uses.

For superconducting qubits, the most extensively studied and, until today, most practical QEC code with scalable error protection is the Surface Code (Kitaev, 1997). Its stabilizer checks are local on a 2D square grid lattice, and with that, it can be realized using nearest-neighbor two-qubit gates, making implementation compatible with superconducting chips with nearest-neighbor couplers.

The simplicity of the Surface Code comes at a price: its comparably high overhead. To encode a single logical qubit into the Surface Code with distance 𝑑, a number of 𝑑²; physical qubits are required.

New hardware approaches like IQM’s star topology (see here) and constellation (see here) raise the hope that superconducting chips can support codes with relaxed locality requirements compared to the Surface Code.

In our paper, we investigate how much we can gain in terms of efficiency by slightly relaxing the connectivity requirement of the Surface Code: More precisely, we present the first general construction for generalizations of the surface with relaxed connectivity requirements.

Our results demonstrate that for the same code distance, Tile Codes can reduce physical qubit counts by more than an order of magnitude (>10× per logical qubit) against the Surface Code, ultimately enabling IQM to build quantum computers that are more than 10 times cheaper than a comparable quantum computer based on the Surface Code. Like the Surface Code, the error protection capability of a Tile Code can be scaled up simply by enlarging the size of the lattice of physical qubits.

Together with IQM’s novel hardware components, Tile Codes therefore pave the way to native qLDPC codes on IQM’s superconducting chips.

 

Tile Codes: Construction

Tile Codes follow a simple and general construction. We will now give an overview of the construction of Tile Codes from a technical perspective.

In the first step, one chooses some stabilizer tiles that resemble the shape of the stabilizer generators. How the stabilizer tiles look will ultimately determine the connectivity we require of the chip. In addition, there is a theoretical condition called topological order on the exact look of the stabilizer tiles, which we explain in depth in the article. An example of a valid pair of stabilizer Tiles looks as follows:

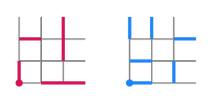
Here, edges correspond to physical qubits; the highlighted edges indicate the stabilizer support.

In the next step, one needs to choose the underlying lattice of qubits and so-called bulk stabilizers. We observe that the best results can be obtained by just picking a regular square layout of bulk stabilizers, as shown below.

Finally, to achieve good error correction capabilities, one needs to add boundary stabilizer tiles: These are stabilizer tiles that are cut off at the boundary of the lattice. One key challenge we resolve in our article is the choice of these boundary stabilizer tiles such that the result is a well-defined CSS code with good error correction properties.

 

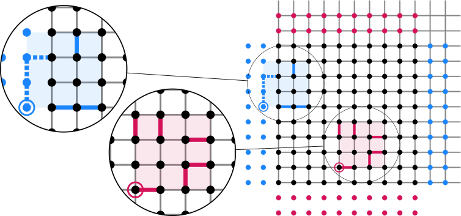
Testing the described procedure on all possible weight-6 and weight-8 stabilizer tiles with modest non-locality, we observe that Tile Codes constructed from our method drastically outperform the Surface Code by a factor of up to 12.7: To implement a logical qubit at the same distance 𝑑 , one needs to use up to 12.7× fewer physical qubits.

 

 

Follow-up work on Tile Codes

Although only made public a few months ago, the Tile Codes have sparked follow-up work that further showcases their potential:

A recent study compares different proposals for qLDPC codes for superconducting hardware and make estimates about the hardware costs. This preliminary study finds that the open boundaries of Tile Codes give a significant improvement in terms of hardware cost compared to their periodic siblings, the BB codes.

Implementability of a QEC code alone is not sufficient for usability in real-world cases: It is crucial to have implementable fault-tolerant protocols to do logical operations on the encoded quantum bits. Another follow-up study to our work demonstrates that due to the remarkably nice structure of the logical operators of Tile Codes, gates between the logical qubits on Tile Codes are possible without introducing any additional connectivity requirements for the hardware and with modest overhead.

 

Conclusion

With the Tile Codes we discovered the so far most promising candidates of qLDPC codes for superconducting hardware. They are constructed to be suitable for the topology of superconducting chips and, with that, promise strong hardware savings. Moreover, performing logical operations on them does not impose further connectivity requirements.