In the race to realize practical quantum computers, noise remains one of the biggest hurdles. Even modest levels of individual gate errors can drastically skew quantum computation results when executing a deep quantum circuit.
Although quantum error correction is a long-term solution, near-term and mid-term quantum devices benefit tremendously from error mitigation—techniques that improve the accuracy of noisy outcomes without the physical-qubit overhead of error correction.
Various quantum error mitigation strategies exist, broadly categorized into noise-aware and noise-agnostic approaches. Noise-aware methods, such as Probabilistic Error Cancellation, require detailed noise characterization, which is challenging due to noise drifts and the complexity of learning Pauli noise. Noise-agnostic methods like Zero Noise Extrapolation (ZNE) avoid explicit noise models but their accuracy is limited by various forms of model mismatch problem. For ZNE, this includes mismatch between the fitting model and the true noise-scaling of the observable of interest as well as uncertainties in noise amplification. Despite significant progress, achieving a reliable noise-agnostic error mitigation framework has been an open challenge.
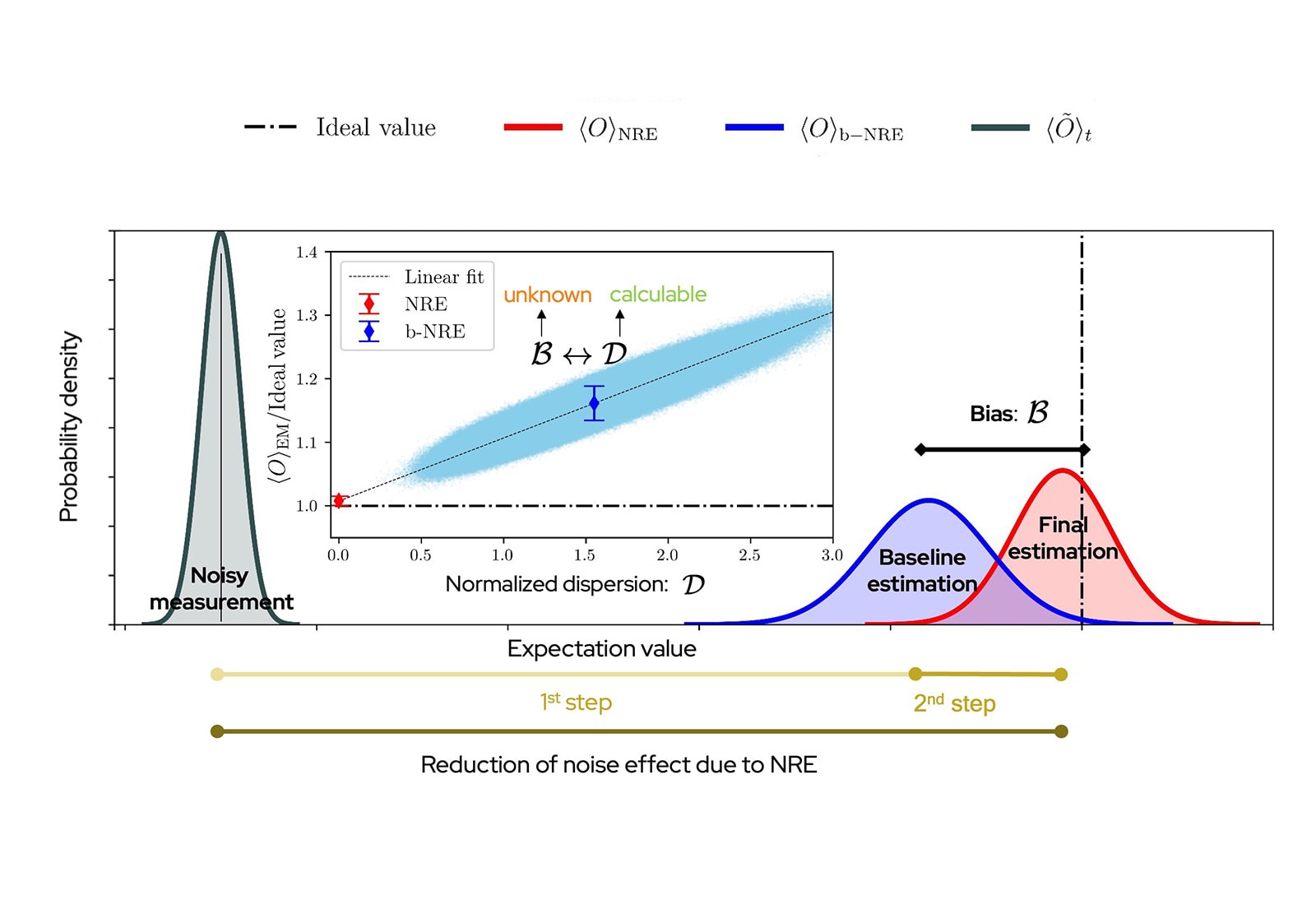
Noise-Robust Estimation is a noise-agnostic error mitigation framework that systematically reduces estimation bias (i.e. the difference between the error-mitigated estimation and the true noiseless value). A key feature of NRE is the discovery of a statistical correlation between the residual bias in quantum expectation value estimations and a measurable quantity called normalized dispersion. This correlation allows for bias suppression without requiring an explicit noise model or assumptions about noise characteristics.
NRE introduces an ansatz where an auxiliary quantity is used to estimate the expectation value of interest. This auxiliary quantity is designed to be less sensitive to noise than the directly measured expectation value of the observable. Unlike existing methods, NRE employs a two-step post-processing framework to achieve robust estimations.
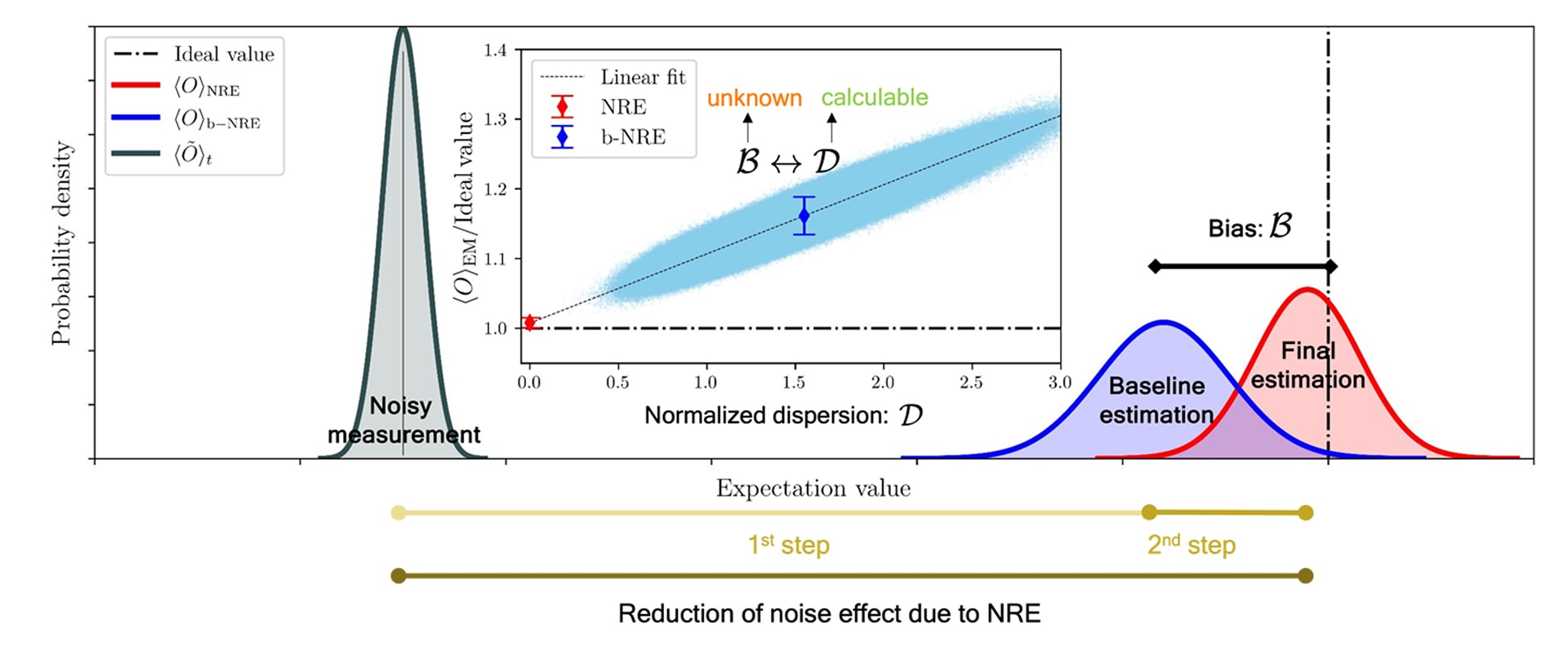
Fig. 1 - Main: Schematic probability density of the noisy measurement, as well as the baseline and final estimation of the NRE framework. Inset: an experimentally obtained example for the correlation between the normalized dispersion and the bias of baseline estimation. The shaded area shows 8 million baseline estimations obtained by bootstrapping. The blue and red data points show the (mean and standard deviation of the) baseline and final estimation.
We tested NRE on an IQM superconducting quantum processor, evaluating circuits with up to 20 qubits and 240 entangling CZ gates for a problem involving measuring ground state energy of Transverse Field Ising Model (TFIM).
The results were striking—NRE consistently outperformed standard quantum error mitigation techniques, including Zero Noise Extrapolation (ZNE), Clifford Data Regression (CDR), variable-noise Clifford Data Regression (vnCDR) and Mitigating Depolarizing-Noise (MDN) with noise-estimation circuits. Across various implementation settings, NRE achieved near bias-free estimations, setting a new benchmark for noise-agnostic error mitigation.
Additionally, NRE demonstrated its effectiveness in quantum chemistry applications, accurately recovering the ground-state energy of the H4 molecule despite severe noise
degradation due to high depth of the circuits involved. Yet, NRE successfully restored the correct energy with high accuracy close to chemical accuracy.
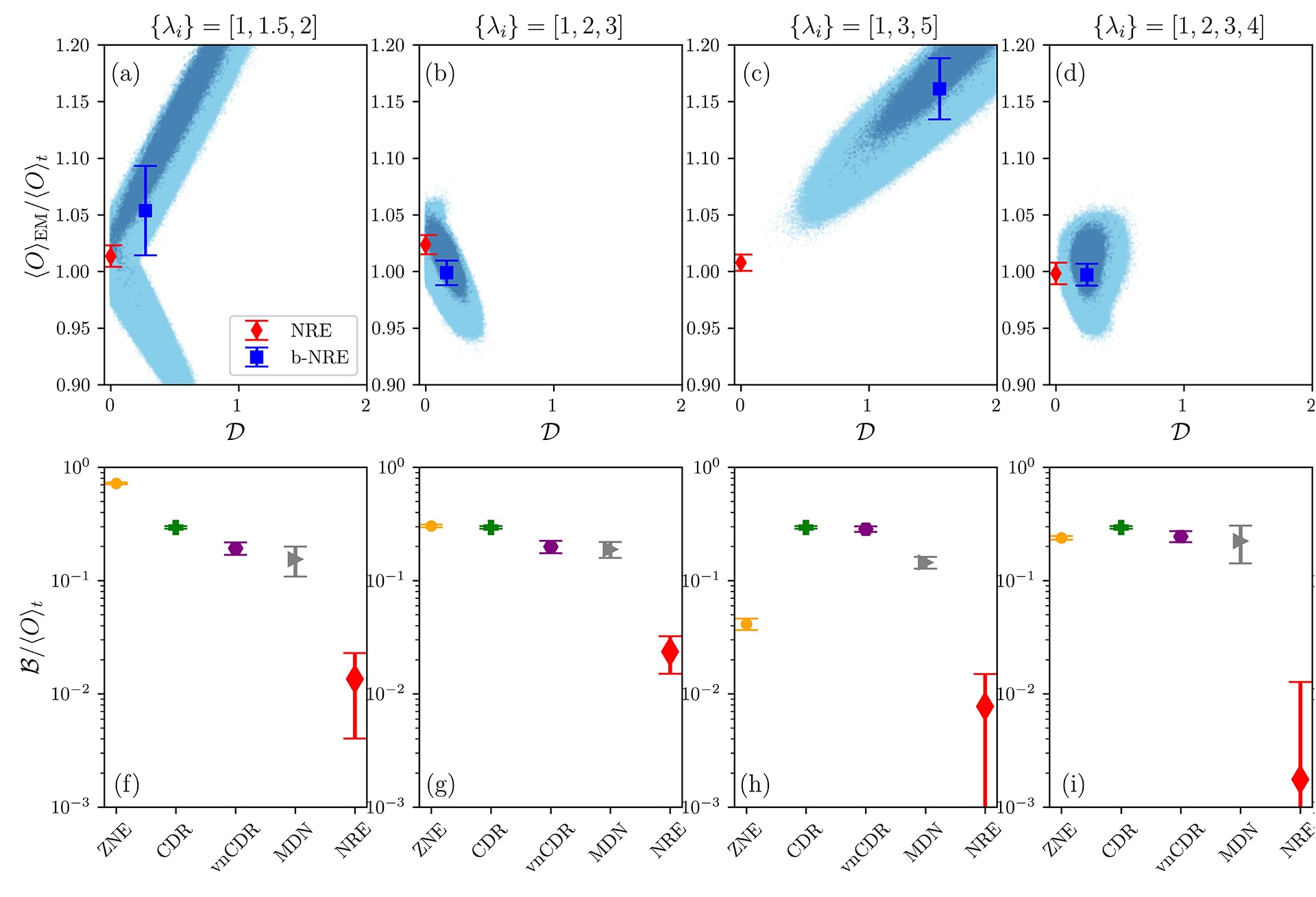
Fig. 2 – NRE Implementation for the ground state energy of Transverse Field Ising Model in paramagnetic phase.
(a-d) Experimentally observed correlation between the bias of the baseline estimation and the normalized dispersion for different noise-amplification settings, {𝜆𝑖}. The y-axis shows the error mitigated outcome 〈𝑂〉EM relative to the noiseless value 〈𝑂〉𝑡. The shaded areas show the baseline estimations obtained via bootstrapping. (f-i) Remaining bias error relative to the noiseless value after performing error mitigation for different error mitigation techniques and different noise-amplification settings. NRE persistently outperforms other methods, and it reduces the bias error up to two orders of magnitude more than any other approach.
As quantum hardware continues to evolve, error mitigation will remain crucial in bridging the gap between noisy intermediate-scale quantum devices and practical quantum computing. NRE not only establishes a new approach in noise mitigation but also opens the door to future refinements, such as:
By continuing to develop these techniques, NRE could become a key tool in pushing quantum devices toward real-world applications.
Please read the NRE paper for further details here: arXiv:2503.06695
